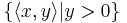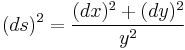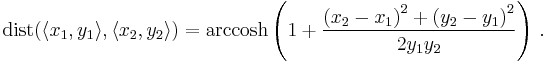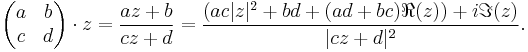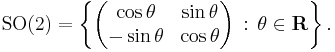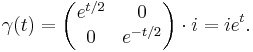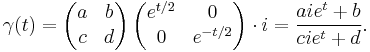Poincaré half-plane model

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane (denoted below as H), together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.

It is named after Henri Poincaré, but originated with Eugenio Beltrami, who used it, along with the Klein model and the Poincaré disk model (due to Riemann), to show that hyperbolic geometry was equiconsistent with Euclidean geometry. The disk model and the half-plane model are isomorphic under a conformal mapping.

1 Metric
2 Special curves
- 2.1 Constructing the curves
3 Symmetry groups
4 Isometric symmetry
5 Geodesics
6 See also
7 References

Metric

The metric of the model on the half-plane

$\{ \langle x, y \rangle | y > 0 \} \,$

is given by

$(d s)^2 = \frac{(d x)^2 %2B (d y)^2}{y^2} \,$

where s measures length along a possibly curved line. The straight lines in the hyperbolic plane (geodesics for this metric tensor, i.e. curves which minimize the distance) are represented in this model by circular arcs perpendicular to the x-axis (half-circles whose origin is on the x-axis) and straight vertical lines ending on the x-axis. The distance between two points measured in this metric along such a geodesic is

$\operatorname{dist} (\langle x_1, y_1 \rangle, \langle x_2, y_2 \rangle) = \operatorname{arccosh} \left( 1 %2B \frac{ {(x_2 - x_1)}^2 %2B {(y_2 - y_1)}^2 }{ 2 y_1 y_2 } \right) \,.$

This model is conformal which means that the angles measured at a point are the same in the model as they are in the actual hyperbolic plane.

This can be generalized to model an n+1 dimensional hyperbolic space by replacing the real number x by a vector in an n dimensional Euclidean vector space.

Special curves

In addition to the straight lines mentioned above, there are other special curves on the hyperbolic plane which can be modeled in the Euclidean half-plane:

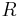A circle (curve equidistant from a central point) with center $\langle x, y \rangle \,$ and radius $R \,$ is modeled by a circle with center 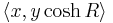$\langle x, y \cosh R \rangle \,$ and radius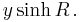 $y \sinh R \,.$
A curve equidistant from a straight line is modeled by either a circular arc which intersects the x-axis at the same two points as the half-circle which models the given line, or by a straight line which intersects the x-axis at the same point as the vertical line which models the given line.
An oricircle (a curve which is like a circle with an infinite radius) is modeled by a circle tangent to the x-axis (but excluding the point of intersection), or by a line parallel to the x-axis. An oricircle is a limit on one side of a sequence of ever larger circles tangent at the same point to a given line; on the other side it is a limit of a sequence of curves equidistant from straight lines which are ever further away.

Constructing the curves

Here is how one can use compass and straightedge constructions in the model to achieve the effect of the basic constructions in the hyperbolic plane. For example, how to construct the half-circle in the Euclidean half-plane which models a line on the hyperbolic plane through two given points.

Creating the line through two existing points:

Draw the line segment between the two points. Construct the perpendicular bisector of the line segment. Find its intersection with the x-axis. Draw the circle around the intersection which passes through the given points. Erase the part which is on or below the x-axis.

Or in the special case where the two given points lie on a vertical line, draw that vertical line through the two points and erase the part which is on or below the x-axis.

Creating the circle through one point with center another point:

Draw the radial line (half-circle) between the two given points as in the previous case. Construct a tangent to that line at the non-central point. Drop a perpendicular from the given center point to the x-axis. Find the intersection of these two lines to get the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.

Or if the two given points lie on a vertical line and the given center is above the other given point, then draw a horizontal line through the non-central point. Draw a circle around the intersection of the vertical line and the x-axis which passes through the given central point. Construct the tangent to that circle at its intersection with the horizontal line. The midpoint between the intersection of the tangent with the vertical line and the given non-central point is the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.

Or if the two given points lie on a vertical line and the given center is below the other given point, then draw a circle around the intersection of the vertical line and the x-axis which passes through the given central point. Draw a line tangent to the circle which passes through the given non-central point. Draw a horizontal line through that point of tangency and find its intersection with the vertical line. The midpoint between that intersection and the given non-central point is the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.

Creating the point which is the intersection of two existing lines, if they intersect:

Find the intersection of the two given semicircles (or vertical lines).

Creating the one or two points in the intersection of a line and a circle (if they intersect):

Find the intersection of the given semicircle (or vertical line) with the given circle.

Creating the one or two points in the intersection of two circles (if they intersect):

Find the intersection of the two given circles.

Symmetry groups

The projective linear group PGL(2,C) acts on the Riemann sphere by the Möbius transformations. The subgroup that maps the upper half-plane, H, onto itself is PSL(2,R), the transforms with real coefficients, and these act transitively and isometrically on the upper half-plane, making it a homogeneous space.

There are four closely related Lie groups that act on the upper half-plane by fractional linear transformations and preserve the hyperbolic distance.

The special linear group SL(2,R) which consists of the set of 2×2 matrices with real entries whose determinant equals +1. Note that many texts (including Wikipedia) often say SL(2,R) when they really mean PSL(2,R).
The group S*L(2,R) consisting of the set of 2×2 matrices with real entries whose determinant equals +1 or −1. Note that SL(2,R) is a subgroup of this group.
The projective special linear group PSL(2,R) = SL(2,R)/{±I}, consisting of the matrices in SL(2,R) modulo plus or minus the identity matrix.
The group PS^*L(2,R) = S^*L(2,R)/{±I}=PGL(2,R) is again a projective group, and again, modulo plus or minus the identity matrix. PSL(2,R) is contained as an index-two normal subgroup, the other coset being the set of 2×2 matrices with real entries whose determinant equals −1, modulo plus or minus the identity.

The relationship of these groups to the Poincaré model is as follows:

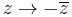The group of all isometries of H, sometimes denoted as Isom(H), is isomorphic to PS^*L(2,R). This includes both the orientation preserving and the orientation-reversing isometries. The orientation-reversing map (the mirror map) is $z\rightarrow -\overline{z}$ .
The group of orientation-preserving isometries of H, sometimes denoted as Isom⁺(H), is isomorphic to PSL(2,R).

Important subgroups of the isometry group are the Fuchsian groups.

One also frequently sees the modular group SL(2,Z). This group is important in two ways. First, it is a symmetry group of the square 2x2 lattice of points. Thus, functions that are periodic on a square grid, such as modular forms and elliptic functions, will thus inherit an SL(2,Z) symmetry from the grid. Second, SL(2,Z) is of course a subgroup of SL(2,R), and thus has a hyperbolic behavior embedded in it. In particular, SL(2,Z) can be used to tessellate the hyperbolic plane into cells of equal (Poincaré) area.

Isometric symmetry

The group action of the projective special linear group PSL(2,R) on H is defined by

$\left(\begin{matrix}a&b\\ c&d\\ \end{matrix}\right) \cdot z = \frac{az%2Bb}{cz%2Bd} = {(ac|z|^2%2Bbd%2B(ad%2Bbc)\Re(z)) %2B i\Im(z)\over|cz%2Bd|^2}.$

Note that the action is transitive, in that for any 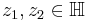$z_1,z_2\in\mathbb{H}$ , there exists a 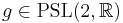$g\in {\rm PSL}(2,\mathbb{R})$ such that 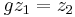$gz_1=z_2$ . It is also faithful, in that if 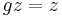$gz=z$ for all z in H, then g=e.

The stabilizer or isotropy subgroup of an element z in H is the set of 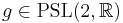$g\in{\rm PSL}(2,\mathbb{R})$ which leave z unchanged: gz=z. The stabilizer of i is the rotation group

${\rm SO}(2) = \left\{ \left(\begin{matrix}\cos\theta&\sin\theta\\ -\sin\theta&\cos\theta\\ \end{matrix}\right)\,:\,\theta\in{\mathbf R}\right\}.$

Since any element z in H is mapped to i by an element of PSL(2,R), this means that the isotropy subgroup of any z is isomorphic to SO(2). Thus, H = PSL(2,R)/SO(2). Alternatively, the bundle of unit-length tangent vectors on the upper half-plane, called the unit tangent bundle, is isomorphic to PSL(2,R).

The upper half-plane is tessellated into free regular sets by the modular group SL(2,Z).

Geodesics

The geodesics for this metric tensor are circular arcs perpendicular to the real axis (half-circles whose origin is on the real axis) and straight vertical lines ending on the real axis.

The unit-speed geodesic going up vertically, through the point i is given by

$\gamma(t) = \left(\begin{matrix}e^{t/2}&0\\ 0&e^{-t/2}\\ \end{matrix}\right) \cdot i = ie^t.$

Because PSL(2,R) acts transitively by isometries of the upper half-plane, this geodesic is mapped into the other geodesics through the action of PSL(2,R). Thus, the general unit-speed geodesic is given by

$\gamma(t) = \left(\begin{matrix}a&b\\ c&d\\ \end{matrix}\right) \left(\begin{matrix}e^{t/2}&0\\ 0&e^{-t/2}\\ \end{matrix}\right) \cdot i = \frac {aie^t %2Bb} {cie^t %2Bd}.$

This provides the complete description of the geodesic flow on the unit-length tangent bundle (complex line bundle) on the upper half-plane.

References

Eugenio Beltrami, Teoria fondamentale degli spazi di curvatura constante, Annali. di Mat., ser II 2 (1868), 232–255
Henri Poincaré (1882) "Théorie des Groupes Fuchsiens", Acta Mathematica v.1, p. 1. First article in a legendary series exploiting the half-plane model. An archived copy is freely available. On page 52 one can see an example of the semicircle diagrams so characteristic of the model.
Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. ISBN 0-387-90465-4.
Jurgen Jost, Compact Riemann Surfaces (2002), Springer-Verlag, New York. ISBN 3-540-43299-X (See Section 2.3).
Saul Stahl, The Poincaré Half-Plane, Jones and Bartlett, 1993, ISBN 0-86720-298-X.
John Stillwell (1998) Numbers and Geometry,pp. 100–104, Springer-Verlag,NY ISBN 0-387-98289-2 .An elementary introduction to the Poincaré half-plane model of the hyperbolic plane.